
Tailoring internal models
Swiss Re’s Pablo Koch Medina, Frank Krieter and Stephan Schreckenberg highlight the key features and main limitations of internal risk models for insurers
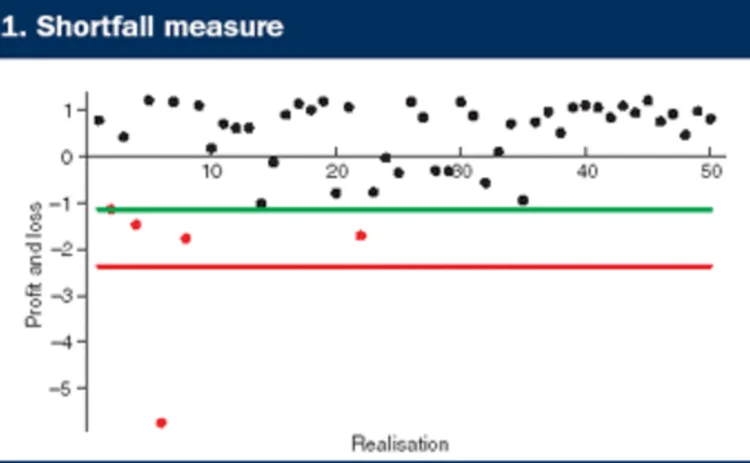
Internal models
Only users who have a paid subscription or are part of a corporate subscription are able to print or copy content.
To access these options, along with all other subscription benefits, please contact info@risk.net or view our subscription options here: http://subscriptions.risk.net/subscribe
You are currently unable to print this content. Please contact info@risk.net to find out more.
You are currently unable to copy this content. Please contact info@risk.net to find out more.
Copyright Infopro Digital Limited. All rights reserved.
As outlined in our terms and conditions, https://www.infopro-digital.com/terms-and-conditions/subscriptions/ (point 2.4), printing is limited to a single copy.
If you would like to purchase additional rights please email info@risk.net
Copyright Infopro Digital Limited. All rights reserved.
You may share this content using our article tools. As outlined in our terms and conditions, https://www.infopro-digital.com/terms-and-conditions/subscriptions/ (clause 2.4), an Authorised User may only make one copy of the materials for their own personal use. You must also comply with the restrictions in clause 2.5.
If you would like to purchase additional rights please email info@risk.net
More on Risk management
Why AI will never predict financial markets
Laws that govern swings in asset prices are beyond statistical grasp of machine learning technology, argues academic Daniel Bloch
Caramanli quits Ion, destination unknown
Current markets head Oliviero is said to have replaced outgoing chief product officer
Treasury selloff challenges back-office systems, data feeds
FIS and Trading Technologies suffered downtime during peak activity
Market whipsaw spurs calls to rethink buy-side stress-testing
Risk Live Boston: Morgan Stanley and BlackRock urge rethink of scenario assumptions and top-down factor models
Top 10 op risks: AI arms race leaves risk teams playing catch-up
As firms invest for fear of being left behind, op risk managers urge caution on data, controls and access
Deutsche’s Americas CRO on risk-taking in choppy markets
Risk Live Boston: Risk managers must stay alive to sudden market moves, but volatility can also bring opportunity, says Jonathan Hummel
Tariff turbulence piles pressure on banks’ VAR models
Backtesting breaches start to mount, but too early to tell if regulatory intervention needed
Ice eyes year-end launch for Treasury clearing service
Third entrant expects Q2 comment period for new access models that address ‘done-away’ accounting hurdle
Most read
- Trump tariffs turn swap spreads into ‘pain trade’
- Inside the week that shook the US Treasury market
- FX liquidity ‘worse than Covid’ amid tariff volatility, dealers say

















